Contoh Soal dan Jawaban Metode Kuadrat Terkecil

Metode kuadrat terkecil (least square method) adalah metode yang dimaksudkan agar jumlah kuadrat dari semua deviasi antara variabel X dan Y yang masing-masing punya koordinat sendiri akan berjumlah seminimal mungkin.

Dari persamaan Y = a + bX, dibuat persamaan:
ΣY = na + bΣX
ΣXY = aΣX + bΣX2

Contoh soal metode kuadrat terkecil:

1. Dari sebuah industri batik diperoleh data produksi dan penjualan sebagai berikut:

Pertanyaan:
a. Buatlah trend produksi dengan metode least square method
b. Tentukan estimasi produksi pada tahun 2004

Jawaban:
Dari soal diatas (tahun 1999 akan kita jadikan tahun dasar dan kita cari estimasi produksi di tahun 2004), maka:

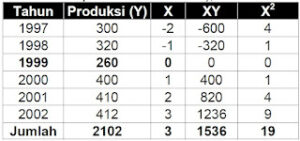
Lalu kita akan melakukan eliminasi dengan cara:

b = 27,714, disubstitusukan ke persamaan:
2102     = 6a + 3b
2102     = 6a + 3(27,714)
2102     = 6a + 83,142
6a          = 2102 – 83,142
a            = 2108,858/6
= 336,476

Jadi persamaan trend produksi dengan metode Least Square adalah: Y = 336,476 + 27,714X

Sehingga estimasi produksi untuk tahun 2004 (X=5) adalah:
Y = 336,476 + 27,714X
Y = 336,476 + 27,714(5)
Y = 336,476 + 138,57
= 475,046

Akhirnya diketahui estimasi produksi untuk tahun 2004 sebanyak 475,046 unit

2. Berikut adalah perkembangan asset pemerintah Indonesia tahun 2014 – 2020 (sumber: https://kemenkeu.go.id), tentukan trend perkembangan nilai asset dan estimasi nilai aset tahun 2030 dengan menggunakan least square method:

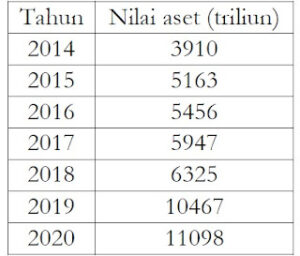
Jawaban:
Buat tabel kolom baru, beri nama X, XY, dan dan X². Lalu hitung nilainya.

Selanjutnya kita cari nilai a dan b:

Maka persamaan trendnya adalah Y = 6909,42 + 1180,03X

Sehingga estimasi nilai aset tahun tahun 2030 (X = 13) adalah:

y =a+bX
=6909,42+1180,03 (13)
=22249.81

Jadi estimasi aset pada tahun 2030 dengan least square method adalah 22249,81 triliun

Setelah membaca artikel ini, kami harap sobat tidak bingung lagi dalam menyelesaikan soal-soal least square method.